分布式图计算
在介绍GraphX之前,我们需要先了解分布式图计算框架。简言之,分布式图框架就是将大型图的各种操作封装成接口,让分布式存储、并行计算等复杂问题对上层透明,从而使工程师将焦点放在图相关的模型设计和使用上,而不用关心底层的实现细节。
分布式图框架的实现需要考虑两个问题,第一是怎样切分图以更好的计算和保存;第二是采用什么图计算模型。下面分别介绍这两个问题。
1 图切分方式
图的切分总体上说有点切分和边切分两种方式。
点切分:通过点切分之后,每条边只保存一次,并且出现在同一台机器上。邻居多的点会被分发到不同的节点上,增加了存储空间,并且有可能产生同步问题。但是,它的优点是减少了网络通信。
边切分:通过边切分之后,顶点只保存一次,切断的边会打断保存在两台机器上。在基于边的操作时,对于两个顶点分到两个不同的机器的边来说,需要进行网络传输数据。这增加了网络传输的数据量,但好处是节约了存储空间。
以上两种切分方式虽然各有优缺点,但是点切分还是占有优势。GraphX以及后文提到的Pregel、GraphLab都使用到了点切分。
2 图计算框架
图计算框架基本上都遵循分布式批同步(Bulk Synchronous Parallell,BSP)计算模式。基于BSP模式,目前有两种比较成熟的图计算框架:Pregel框架和GraphLab框架。
2.1 BSP
2.1.1 BSP基本原理
在BSP中,一次计算过程由一系列全局超步组成,每一个超步由并发计算、通信和同步三个步骤组成。同步完成,标志着这个超步的完成及下一个超步的开始。
BSP模式的准则是批量同步(bulk synchrony),其独特之处在于超步(superstep)概念的引入。一个BSP程序同时具有水平和垂直两个方面的结构。从垂直上看,一个BSP程序由一系列串行的超步(superstep)组成,如图所示:
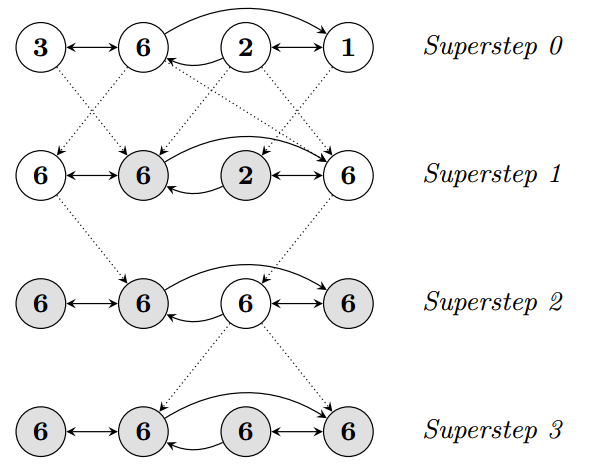
从水平上看,在一个超步中,所有的进程并行执行局部计算。一个超步可分为三个阶段,如图所示:
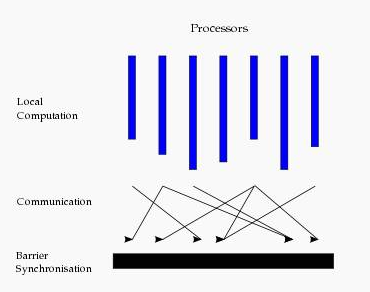
- 本地计算阶段,每个处理器只对存储在本地内存中的数据进行本地计算。
- 全局通信阶段,对任何非本地数据进行操作。
- 栅栏同步阶段,等待所有通信行为的结束。
2.1.2 BSP模型特点
BSP模型有如下几个特点:
1 将计算划分为一个一个的超步(
superstep),有效避免死锁;2 将处理器和路由器分开,强调了计算任务和通信任务的分开,而路由器仅仅完成点到点的消息传递,不提供组合、复制和广播等功能,这样做既掩盖具体的互连网络拓扑,又简化了通信协议;
3 采用障碍同步的方式、以硬件实现的全局同步是可控的粗粒度级,提供了执行紧耦合同步式并行算法的有效方式
2.2 Pregel框架
Pregel是一种面向图算法的分布式编程框架,采用迭代的计算模型:在每一轮,每个顶点处理上一轮收到的消息,并发出消息给其它顶点,并更新自身状态和拓扑结构(出、入边)等。
2.2.1 Pregel框架执行过程
在Pregel计算模式中,输入是一个有向图,该有向图的每一个顶点都有一个相应的由字符串描述的vertex identifier。每一个顶点都有一些属性,这些属性可以被修改,其初始值由用户定义。每一条有向边都和其源顶点关联,并且也拥有一些用户定义的属性和值,并同时还记录了其目的顶点的ID。
一个典型的Pregel计算过程如下:读取输入,初始化该图,当图被初始化好后,运行一系列的超步,每一次超步都在全局的角度上独立运行,直到整个计算结束,输出结果。
在每一次超步中,顶点的计算都是并行的,并且执行用户定义的同一个函数。每个顶点可以修改其自身的状态信息或以它为起点的出边的信息,从前序超步中接受消息,并传送给其后续超步,或者修改整个图的拓扑结构。边,在这种计算模式中并不是核心对象,没有相应的计算运行在其上。
算法是否能够结束取决于是否所有的顶点都已经vote标识其自身已经达到halt状态了。在superstep 0中,所有顶点都置于active状态,每一个active的顶点都会在计算的执行中在某一次的superstep中被计算。顶点通过将其自身的状态设置成halt来表示它已经不再active。这就表示该顶点没有进一步的计算需要进行,除非被其他的运算触发,而Pregel框架将不会在接下来的superstep中计算该顶点,除非该顶点收到一个其他superstep传送的消息。
如果顶点接收到消息,该消息将该顶点重新置active,那么在随后的计算中该顶点必须再次deactive其自身。整个计算在所有顶点都达到inactive状态,并且没有消息在传送的时候宣告结束。这种简单的状态机制在下图中描述:
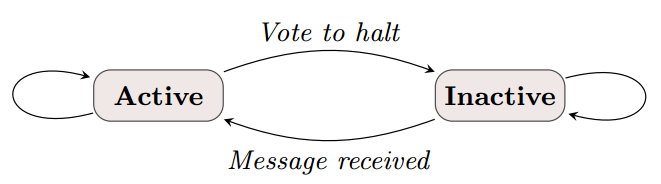
我们用PageRank为例来说明Pregel的计算过程。
def PageRank(v: Id, msgs: List[Double]) {
// 计算消息和
var msgSum = 0
for (m <- msgs) { msgSum = msgSum + m }
// 更新 PageRank (PR)
A(v).PR = 0.15 + 0.85 * msgSum
// 广播新的PR消息
for (j <- OutNbrs(v)) {
msg = A(v).PR / A(v).NumLinks
send_msg(to=j, msg)
}
// 检查终止
if (converged(A(v).PR)) voteToHalt(v)
}
以上代码中,顶点v首先接收来自上一次迭代的消息,计算它们的和。然后使用计算的消息和重新计算PageRank,之后程序广播这个重新计算的PageRank的值到顶点v的所有邻居,最后程序判断算法是否应该停止。
2.2.1 Pregel框架的消息模式
Pregel选择了一种纯消息传递的模式,忽略远程数据读取和其他共享内存的方式,这样做有两个原因。
第一,消息的传递有足够高效的表达能力,不需要远程读取(
remote reads)。第二,性能的考虑。在一个集群环境中,从远程机器上读取一个值是会有很高的延迟的,这种情况很难避免。而消息传递模式通过异步和批量的方式传递消息,可以缓解这种远程读取的延迟。
图算法其实也可以被写成是一系列的链式MapReduce作业。选择不同的模式的原因在于可用性和性能。Pregel将顶点和边在本地机器进行运算,而仅仅利用网络来传输信息,而不是传输数据。
而MapReduce本质上是面向函数的,所以将图算法用MapReduce来实现就需要将整个图的状态从一个阶段传输到另外一个阶段,这样就需要许多的通信和随之而来的序列化和反序列化的开销。另外,在一连串的MapReduce作业中各阶段需要协同工作也给编程增加了难度,这样的情况能够在Pregel的各轮超步的迭代中避免。
2.2.3 Pregel框架的缺点
这个模型虽然简单,但是缺陷明显,那就是对于邻居数很多的顶点,它需要处理的消息非常庞大,而且在这个模式下,它们是无法被并发处理的。所以对于符合幂律分布的自然图,这种计算模型下很容易发生假死或者崩溃。
2.3 GraphLab框架
GraphLab将数据抽象成Graph结构,将基于顶点切分的算法的执行过程抽象成Gather、Apply、Scatter三个步骤。以下面的例子作为一个说明。
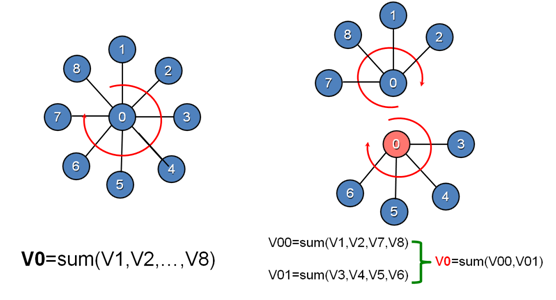
示例中,需要完成对V0邻接顶点的求和计算,串行实现中,V0对其所有的邻接点进行遍历,累加求和。而GraphLab中,将顶点V0进行切分,将V0的边关系以及对应的邻接点部署在两台处理器上,各台机器上并行进行部分求和运算,然后通过master(蓝色)顶点和mirror(橘红色)顶点的通信完成最终的计算。
2.3.1 GraphLab框架的数据模型
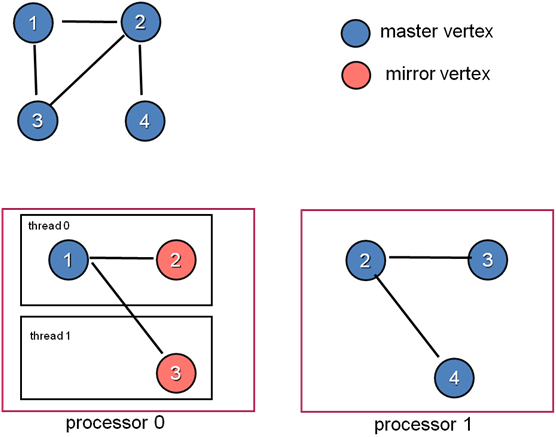
对于分割的某个顶点,它会被部署到多台机器,一台机器作为master顶点,其余机器作为mirror。master作为所有mirror的管理者,负责给mirror安排具体计算任务;mirror作为该顶点在各台机器上的代理执行者,与master数据的保持同步。
对于某条边,GraphLab将其唯一部署在某一台机器上,而对边关联的顶点进行多份存储,解决了边数据量大的问题。
同一台机器上的所有顶点和边构成一个本地图(local graph),在每台机器上,存在一份本地id到全局id的映射表。顶点是一个进程上所有线程共享的,在并行计算过程中,各个线程分摊进程中所有顶点的gather->apply->scatter操作。
我们用下面这个例子说明,GraphLab是怎么构建Graph的。图中,以顶点v2和v3进行分割。顶点v2和v3同时存在于两个进程中,并且两个线程共同分担顶点计算。
2.3.2 GraphLab框架的执行模型
每个顶点每一轮迭代会经过gather -> apple -> scatter三个阶段。
Gather阶段,工作顶点的边从连接顶点和自身收集数据。这一阶段对工作顶点、边都是只读的。
Apply阶段,
mirror将gather阶段计算的结果发送给master顶点,master进行汇总并结合上一步的顶点数据,按照业务需求进行进一步的计算,然后更新master的顶点数据,并同步给mirror。Apply阶段中,工作顶点可修改,边不可修改。Scatter阶段,工作顶点更新完成之后,更新边上的数据,并通知对其有依赖的邻结顶点更新状态。在
scatter过程中,工作顶点只读,边上数据可写。
在执行模型中,GraphLab通过控制三个阶段的读写权限来达到互斥的目的。在gather阶段只读,apply对顶点只写,scatter对边只写。并行计算的同步通过master和mirror来实现,mirror相当于每个顶点对外的一个接口人,将复杂的数据通信抽象成顶点的行为。
下面这个例子说明GraphLab的执行模型:
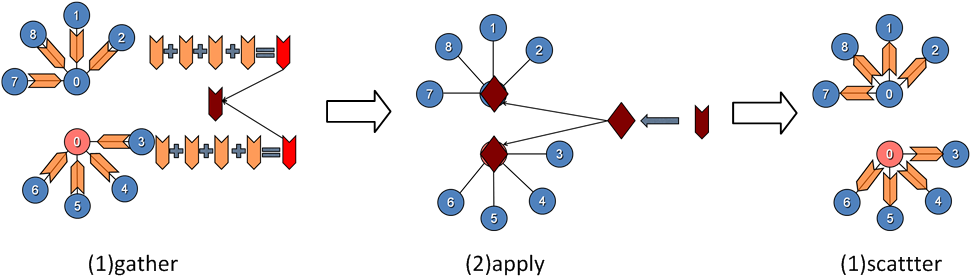
利用GraphLab实现的PageRank的代码如下所示:
//汇总
def Gather(a: Double, b: Double) = a + b
//更新顶点
def Apply(v, msgSum) {
A(v).PR = 0.15 + 0.85 * msgSum
if (converged(A(v).PR)) voteToHalt(v)
}
//更新边
def Scatter(v, j) = A(v).PR / A(v).NumLinks
由于gather/scatter函数是以单条边为操作粒度,所以对于一个顶点的众多邻边,可以分别由相应的节点独立调用gather/scatter函数。这一设计主要是为了适应点分割的图存储模式,从而避免Pregel模型会遇到的问题。
3 GraphX
GraphX也是基于BSP模式。GraphX公开了一个类似Pregel的操作,它是广泛使用的Pregel和GraphLab抽象的一个融合。在GraphX中,Pregel操作者执行一系列的超步,在这些超步中,顶点从之前的超步中接收进入(inbound)消息,为顶点属性计算一个新的值,然后在以后的超步中发送消息到邻居顶点。
不像Pregel而更像GraphLab,消息通过边triplet的一个函数被并行计算,消息的计算既会访问源顶点特征也会访问目的顶点特征。在超步中,没有收到消息的顶点会被跳过。当没有消息遗留时,Pregel操作停止迭代并返回最终的图。